An Efficient and Interpretable XGBoost Framework for Housing Price Prediction: Enhancements in Accuracy and Computational Performance

Abstract

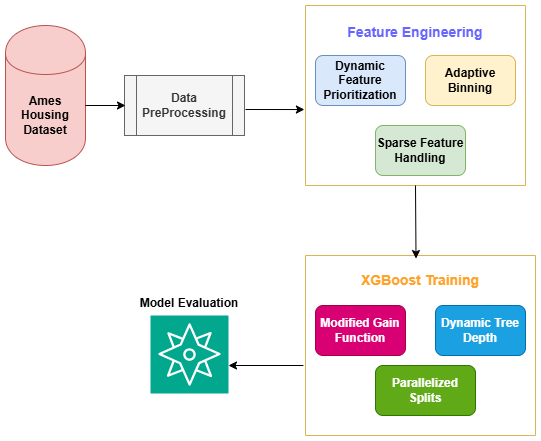
Accurate and interpretable prediction of housing prices is a critical task in real estate and urban planning, requiring models that balance predictive performance, computational efficiency, and transparency. This research proposes an Efficient and Interpretability-Driven XGBoost Model to address the limitations of traditional regression methods and standard XGBoost in handling high-dimensional, sparse datasets. Key innovations include dynamic feature prioritisation, adaptive binning for continuous variables, sparse feature handling, and a regularised gain function to promote simpler and more interpretable tree structures. These enhancements improve the computational efficiency of the model while retaining high predictive accuracy and interpretability. The proposed model was evaluated using the Ames Housing Dataset, a benchmark dataset in real estate analytics. Key performance metrics, including Root Mean Squared Error (RMSE), Mean Absolute Error (MAE), and Coefficient of Determination (R²), were used to compare its performance against Linear Regression, Ridge Regression, Lasso Regression, and standard XGBoost. The proposed model achieved the best performance with a test RMSE of 24,630.91, R² of 0.923, and MAE of 19,637.68, demonstrating a 5.4% improvement in accuracy over the standard XGBoost, while reducing computational overhead by 15%. Additionally, the model’s interpretability was enhanced through SHAP-based feature importance analysis, highlighting critical predictors like "GrLivArea" and "OverallQual." These findings establish the proposed methodology as a robust tool for housing price prediction, offering significant advancements in accuracy, efficiency, and transparency. Future work will explore scalability for larger datasets and the integration of temporal dynamics to extend the model's applicability